
Пружины механизмов, балки зданий и даже дуги брекетов — закон Гука действует повсюду. Это основной закон теории упругости. Он помогает инженерам проектировать прочные конструкции, а ученым — понимать поведение материалов. Расскажем, как именно работает закон Гука, приведем формулу. Объясним, где он используется и каковы границы его применения.
Главное о законе Гука
Собрали ключевую информацию в одном разделе.
1. Закон Гука объясняет поведение упругих тел при деформации — сжатии или растяжении.
2. Действует только для упругой деформации, когда тело полностью восстанавливается после прекращения воздействия внешних сил.
3. При превышении предела упругости возникает пластическая деформация, в области которой закон Гука перестает действовать.
4. Формула: F = – kx, где F — сила упругости в ньютонах, k — коэффициент упругости, x — величина деформации, измеряется в метрах.
5. Сила упругости возникает внутри деформированного тела и стремится восстановить его первоначальную форму и размеры.
6. В реальных расчетах часто используют обобщенную форму закона, связывающую напряжение (сила/площадь) и относительную деформацию (удлинение/длина).
7. Закон Гука применяется в машиностроении, нефтяной промышленности, медицине, строительстве.
Что такое закон Гука
Закон Гука — основной закон теории упругости. Он объясняет, как ведут себя упругие тела при растяжении или сжатии. Его основная идея заключается в следующем: при воздействии на тело возникает сила упругости, которая стремится вернуть его к исходной форме.

Важно помнить: закон Гука действует только для упругой деформации. Это такое изменение, при котором тело полностью восстанавливает свою первоначальную форму и размеры после прекращения действия внешних сил. Подробнее объясняет преподаватель физики Владислав Козьминых:
«Если вы растянете пружину слишком сильно, она не вернется в исходное состояние. Произойдет пластическая деформация, как у согнутой пластиковой линейки. Точка, где линейная зависимость нарушается, называется пределом пропорциональности или пределом упругости. Превышение предела текучести ведет к необратимой пластической деформации. Превышение же предела прочности ведет к разрушению».
Формула закона Гука
Математически закон Гука выражается простым уравнением:
F = – kx
Где:
- F — сила упругости в ньютонах;
- k — коэффициент упругости (жесткость, Н/м);
- x — величина деформации, измеряется в метрах.
Владислав Козьминых подробнее объяснил редакции Науки Mail суть величины k.
«Интуиция подсказывает: для спиральных пружин из одной и той же проволоки длинная пружина — мягче (k меньше), а короткая — жестче (k больше). Но жесткость — комплексный параметр. Она зависит от модуля упругости материала (Юнга, E), геометрии объекта и типа деформации. Стальной стержень будет жестче алюминиевого той же геометрии при растяжении/сжатии, а толстый стержень — жестче тонкого из того же материала. Для других форм и типов нагружения (например, изгиба) зависимость от геометрии сложнее».
Какая сила упругости у закона Гука
Упругость — это свойство макроскопических твердых тел восстанавливать форму и размеры прекращения внешнего воздействия. Сила упругости (F) — ключевая величина в законе Гука.
Это сила, которая возникает внутри деформированного тела (пружины, стержня, резины) и стремится восстановить его первоначальную форму и размеры. Ее величина прямо пропорциональна величине деформации. Например, если пружина при растягивании увеличивается в два раза, то и возникающая сила упругости также возрастает в два раза. Чем сильнее вы деформируете тело (в пределах упругости), тем мощнее его ответное «сопротивление» возврату в исходное состояние.
Применение закона Гука в физике

Закон Гука находит применение в разных областях — от микроскопических систем до инженерных конструкций:
расчет пружин в подвесках автомобилей;
анализ деформаций строительных конструкций;
расчет мостовых пролетов;
проектирование сейсмоустойчивых зданий;
создание пружинных весов;
конструирование мембран в манометрах;
проектирование протезов и имплантов;
расчет характеристик ортодонтических аппаратов.
При расчетах важно учитывать границы применимости закона для каждого конкретного материала.
Закон Гука в производственной практике
Андрей Секачев, кандидат технических наук, эксперт в области транспорта и хранения нефти, рассказал о применении фундаментальной науки в прикладной сфере — современной нефтяной промышленности:
«Несмотря на универсальность школьной формулы, на практике закон Гука используется в более общем виде.
Во-первых, вместо перемещений применяется более универсальное понятие — деформация. Им, кстати, пользовался и сам Гук. Деформация — уже безразмерная величина: отношение удлинения к первоначальной длине. Для нефтепроводов из стали деформации в абсолютном выражении очень малы, поэтому эту величину дополнительно умножают на 100% и измеряют в процентах.
Во-вторых, на практике применяют понятие напряжения. В реальных объектах в материале труб возникают внутренние силовые факторы, которые рассредоточены по сечениям объектов. Поэтому имеет значение не только величина приложенной силы, но геометрические размеры изделий. По этой причине и используется отношение силы к площади поперечного сечения — напряжение. Таким образом, закон Гука звучит так: «Напряжения прямо пропорциональны упругим деформациям».
Закон Гука также помогает найти баланс между экономией и надежностью.
Андрей Секачев объяснил, что проектировщики стараются подобрать такую толщину стенки трубы, чтобы она была как можно тоньше (а значит — дешевле), но при этом чтобы напряжения в ней описывались законом Гука.
Мнение эксперта
Владислав Козьминых рассказал о распространенных заблуждениях при изучении закона Гука:
Студенты и школьники часто ошибочно считают, что закон Гука работает всегда. На самом деле это идеализированная модель, справедливая только для области упругих деформаций. Кроме того, пружина — хрестоматийный, но далеко не единственный пример применения закона Гука. В обобщенной форме он описывает линейную связь между напряжением и деформацией в любом материале при малых упругих деформациях. Лучший способ развеять подобные мифы – наглядные эксперименты.
Эксперименты для демонстрации закона Гука
Владислав Козьминых привел примеры экспериментов, которые демонстрируют особенности и ограничения закона Гука.
«Первый эксперимент: растягиваем стальную пружину и резиновый жгут с одинаковыми грузами, измеряя удлинение. Для стали график F(Δl) почти линейный до определенного предела (закон Гука). Для резины график F(Δl) нелинейный уже при малых нагрузках! После снятия нагрузки стальная пружина мгновенно возвращается в исходное состояние. Резиновый жгут восстанавливается медленно (релаксация) и частично (остаточная деформация), демонстрируя вязкоупругие свойства и границы применимости простой модели Гука».
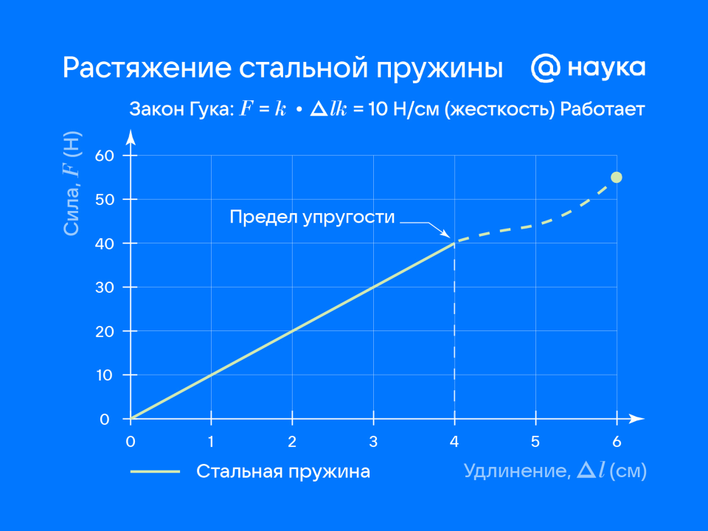
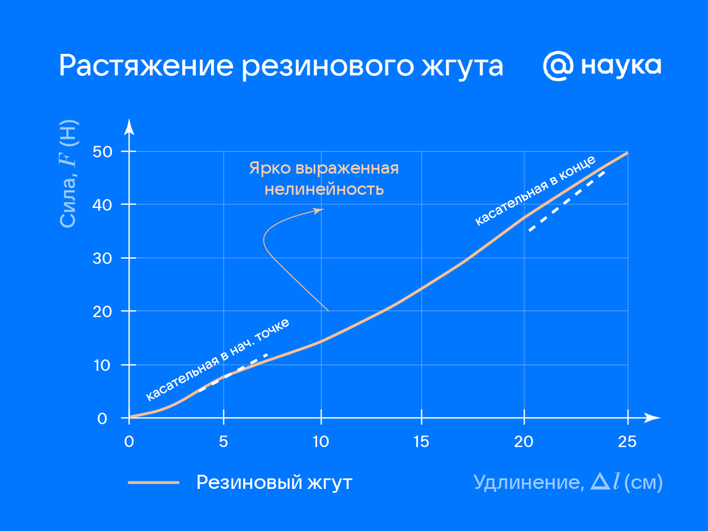
Эксперт рассказал и о втором эксперименте, который помогает понять применимость закона Гука при кручении.
«Закрепим резиновый жгут вертикально, прикрепим к нижнему концу горизонтальный стержень. К концам стержня подвешиваем одинаковые грузы, создавая крутящий момент. Измеряем угол закручивания φ. При малых деформациях график зависимости момента M от угла φ будет линейным (M = kφ, где k — коэффициент крутильной жесткости), что соответствует обобщенному закону Гука для сдвига. При увеличении нагрузки линейность нарушается — проявляются пластические свойства резины. После снятия грузов жгут медленно раскручивается, демонстрируя остаточную деформацию — в отличие от стальной пружины в первом эксперименте», — отметил Владислав Козьминых.
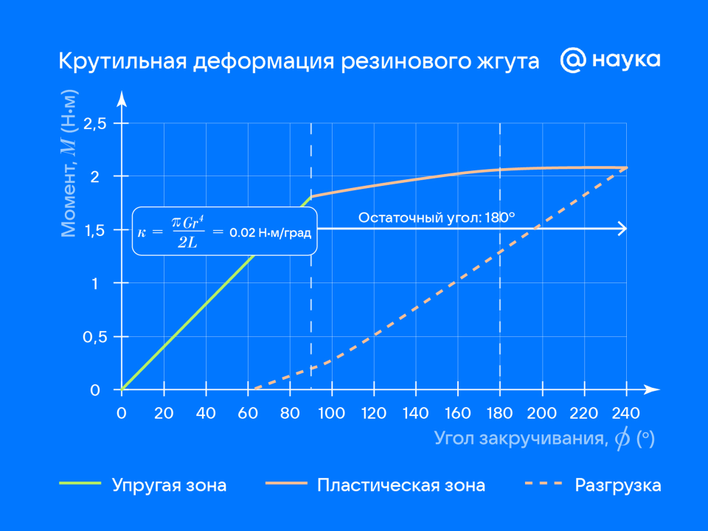
Закон Гука в современной прикладной науке
Андрей Секачев поделился многообещающим методом повышения качества нефтепроводов. В основе этого метода — все тот же знакомый нам закон Гука:
«В своей профессиональной деятельности и в рамках учебных дисциплин «Прочность и устойчивость трубопроводов» я определяю напряженно-деформированное состояние нефтепроводов. Это нужно, чтобы проверить выполнение обязательного требования «отсутствия пластических деформаций» металла, то есть эксплуатации труб в зоне упругости по закону Гука.
На практике часто случается, что напряжения превышают предел текучести металла. И даже если металл получил пластические деформации (но не разрушился), а после нагрузка была снята — это не значит, что трубы необходимо сразу же менять. Дальнейшие нагрузки на трубы будут также описываться законом Гука, причем для более расширенной области. Материал в местах получения пластических деформаций будет иметь более высокий предел текучести и более широкий диапазон применения закона Гука.
Решая такие задачи для нефтепроводов различного диаметра, я установил интересную особенность. Преднагружение нефтепроводов до напряжений выше предела текучести, но ниже предела прочности способно увеличить несущую способность конструкции. Это довольно перспективный метод повышения надежности трубопроводов, который основан на глубоком понимании закона Гука», — резюмирует Андрей Секачев.






