
В теории узлов каждый узел характеризуется числом, которое показывает, сколько пересечений нужно изменить, чтобы полностью распутать его до состояния простой петли. Это число называется числом развязывания. Считалось, что число развязывания сложного узла, полученного соединением двух простых, всегда равно сумме чисел развязывания исходных узлов. Однако недавно это утверждение было опровергнуто. Исследование опубликовано в arXiv.
Математики во главе с Марком Бриттенхэмом выявили, что в некоторых случаях объединение узлов дает узел, который легче распутать, чем предполагалось. Они нашли не просто один такой пример, а бесконечное количество пар узлов, для которых объединенный узел имеет меньшее число развязывания, чем сумма чисел для каждого из составляющих его узлов, сообщает New Scientist.
Мы искали решение, не особенно веря в его существование, ведь гипотеза просуществовала так долго. Это было очень неожиданным и удивительным открытием.
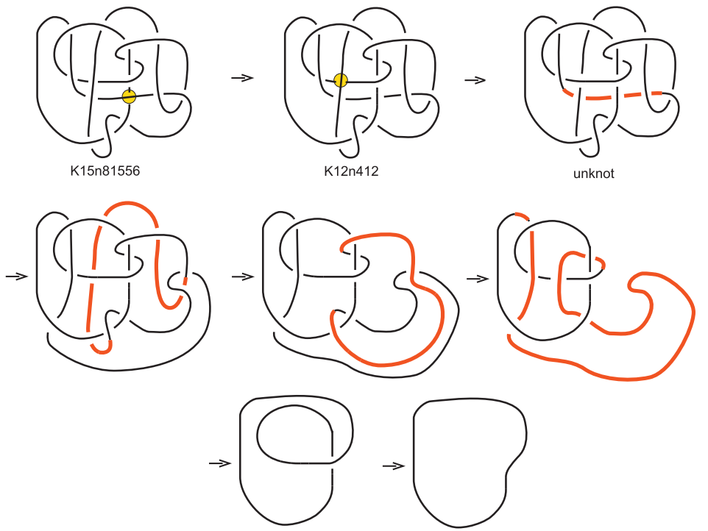
Для проверки своего открытия математики использовали комбинацию теоретических расчетов и практических экспериментов с узлами, завязанными из обычной веревки. Эти простые физические тесты подтвердили расчеты исследователей, показав на практике, что объединенные узлы действительно развязываются проще.
Теперь мы понимаем немного больше о том, как ведут себя петли в трехмерном пространстве, чем несколько месяцев назад.
Исследование открывает перед математикой новые горизонты и показывает, насколько неисчерпаемыми остаются даже классические области математики.
Ранее Наука Mail рассказывала о том, что математики приблизились к числу, за которым край современной теории: это число BB(6), настолько огромное, что его значение может выйти за рамки всей современной математики.
