Многие объекты — от молекул до роботов и элементарных частиц — сохраняют свои свойства при повороте или зеркальном отражении. Современные эквивариантные нейросети способны учитывать такие симметрии при обработке данных, что делает их особенно востребованными в научных и технологических задачах — от моделирования химических соединений до анализа физических процессов и распознавания изображений.
Но у этих моделей есть недостаток: за высокую точность приходится платить сложностью. Они требуют огромного количества обучаемых параметров, что делает их тяжеловесными, требовательными к ресурсам и подверженными переобучению, особенно если данных немного.
Сотрудники департамента математики и Лаборатории геометрической алгебры и приложений факультета экономических наук НИУ ВШЭ Екатерина Филимошина и Дмитрий Широков разработали архитектуру GLGENN (Generalized Lipschitz Group Equivariant Neural Networks), которая решает эту проблему. Она позволяет моделям сохранять симметрии в данных, но при этом требует в разы меньше параметров. Добиться этого авторам помог известный математический аппарат — геометрические алгебры Клиффорда — и оригинальный метод разделения весов, который учитывает внутренние алгебраические структуры данных.
Мы хотели построить модель, которая будет умной, но при этом легкой. GLGENN показывает, что эквивариантные нейросети не обязаны быть громоздкими и сложными. Даже с ограниченными данными они могут обучаться эффективно и без потери качества.
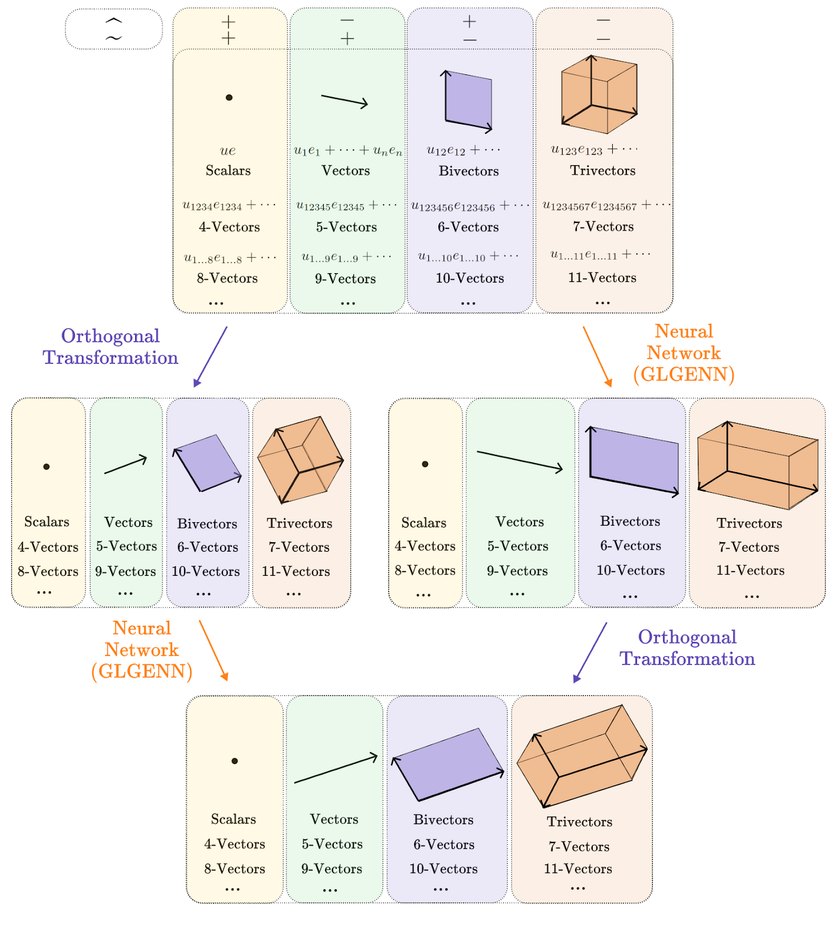
Модель прошла испытания на разнообразных задачах — от симуляции физических процессов до работы с геометрическими данными — и показала результаты, сравнимые или лучшие, чем у существующих методов. При этом GLGENN работает быстрее и эффективнее за счет меньшего числа обучаемых параметров, что делает ее более доступной для практического применения.
Эти результаты могут стать шагом к созданию новых нейросетевых инструментов для науки и техники. Мы уверены, что подход, основанный на геометрических алгебрах, найдет применение в самых разных областях, включая биоинформатику, робототехнику и геоинформатику.
Участие в ICML стало признанием высокого уровня исследований в области машинного обучения, которые ведутся в НИУ ВШЭ. Ученые планируют развивать архитектуру GLGENN, расширяя ее возможности для работы с новыми типами данных, а также исследовать потенциальное применение модели в задачах физики, робототехники и компьютерного зрения.

