
Расскажем, что такое числа Фибоначчи, кто открыл эту последовательность, как она связана с золотым сечением и в каких областях применяется.
Что такое числа Фибоначчи: суть простыми словами
Числа Фибоначчи — это последовательность, где каждое следующее число получается путем сложения двух предыдущих. В классическом варианте она начинается с 0 и 1. Цепочку значений можно продолжать до бесконечности.
Пример:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34…
(0 + 1 = 1
1 + 1 = 2
1 + 2 = 3…)
История открытия чисел Фибоначчи и формула последовательности
История чисел уходит корнями в глубокую древность. Считается, что древнеиндийский математик Пингала использовал их для анализа стихотворных ритмов в санскритской литературе. Позже последовательность изучали в арабском мире, но в Европе о ней узнали благодаря математику эпохи Средневековья Леонардо Пизанскому, или Фибоначчи.
В 1202 году ученый выпустил «Книгу абака» (Liber Abaci) — фундаментальный труд по арифметике. Он рассмотрел широкий круг тем: действия с целыми и дробными числами, разложение на множители и многое другое. В книге была описана задача о размножении кроликов, которая основана на последовательности чисел. Остановимся на ней подробнее.

Условие. В начале есть одна пара кроликов. Каждый месяц пара рождает новую пару. Они начинают размножаться через месяц. Сколько пар будет через один год?
Решение. Количество пар через каждый месяц образует последовательность 1, 1, 2, 3, 5, 8… — это и есть числа Фибоначчи. Ответ: 377 пар.
Хотя задача очень упрощена, она помогла популяризировать последовательность в Европе.
Числа Фибоначчи можно рассчитать по формуле:
F (n) = F (n-1) + F (n-2),
Пример:
F (5) = F (4) + F (3) = 3 + 2 = 5.
В XIX веке французский математик Жак Бине вывел формулу, которая позволяет найти любое число Фибоначчи без расчета предыдущих. В ней используется значение, равное ≈ 1,618, его еще называют золотым сечением и обозначают знаком φ (фи).
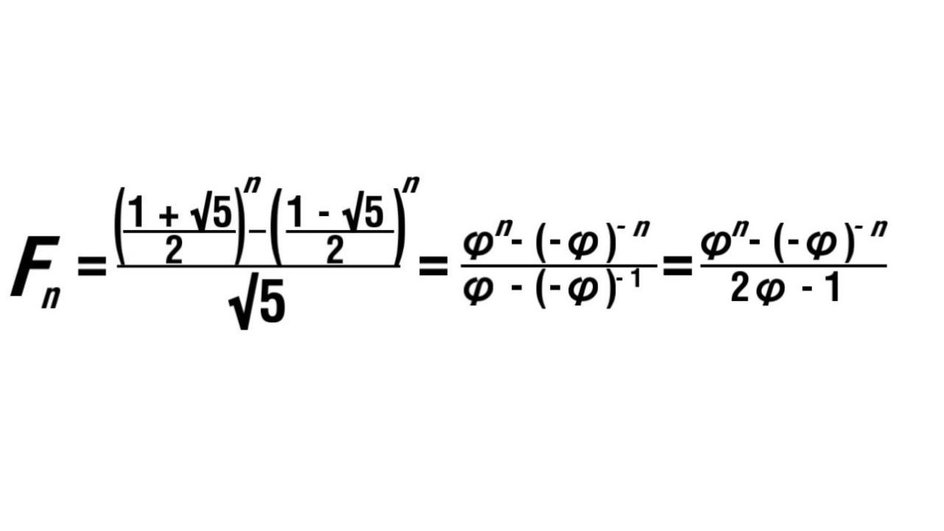
где φ = (1 + √5)/2 — золотое сечение. При этом φ и (-φ)⁻¹ = 1 - φ являются корнями уравнения x² - x - 1 = 0.
Как числа Фибоначчи связаны с золотым сечением
Золотое сечение (≈1,618) — это пропорция, которая тысячелетиями вдохновляла художников, скульпторов и дизайнеров. Ее также называют «формулой совершенства», потому что построенные на этом соотношении объекты кажутся человеческому глазу удивительно гармоничными.
Интересно, но если делить каждое число Фибоначчи на предыдущее, результат постепенно приближается к 1,618.
Пример:
5 : 3 ≈ 1,666
8 : 5 ≈ 1,6
13 : 8 ≈ 1,625
21 : 13 ≈ 1,615
34 : 21 ≈ 1,619
Золотое сечение чаще всего изображают в виде спирали. Для ее построения рисуют квадраты со сторонами, пропорциональными числам Фибоначчи, а затем соединяют их дугами.
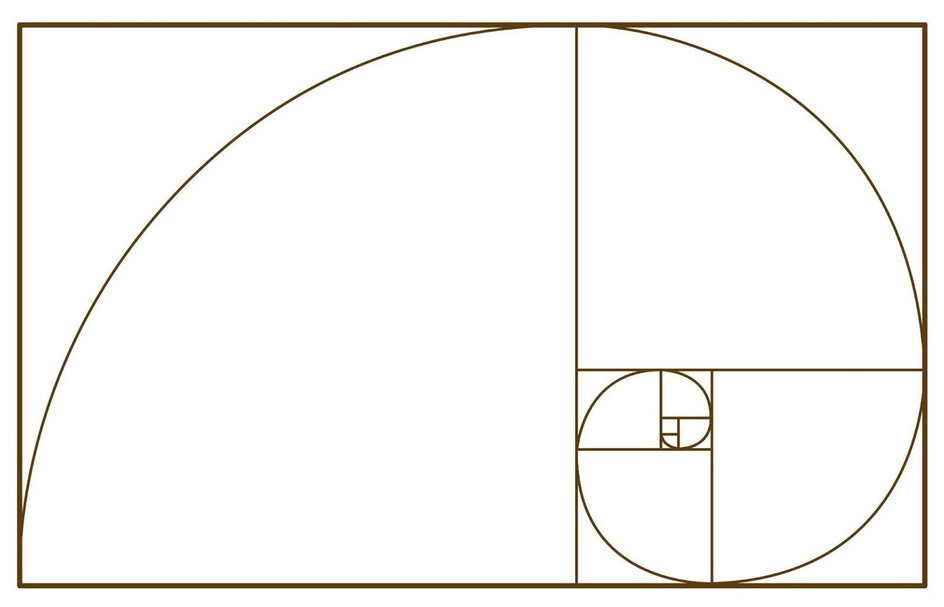
Эталон гармонии и красоты можно встретить в природе. Например, листья на стебле, семена подсолнуха или шишки расположены по спиралям. Если рассмотреть витки раковины наутилуса, то можно заметить, что они приближаются к числу, близкому к значению φ (фи). Каждый новый виток увеличивает раковину примерно в 1,618 раза.
Это объясняется тем, что раковины морских существ растут только в одном направлении. Чтобы избежать чрезмерного удлинения, они закручиваются, при этом каждый следующий виток напоминает предыдущий.

Примеры золотого сечения можно наблюдать в пропорциях человеческого лица. Один из сторонников теории ― пластический хирург Стивен Марквардт ― в 2002 году заявил, что ширина рта должна превышать ширину носа в 1,618 раза. На основе этого принципа Марквардт разработал «маску красоты» — шаблон, который отражает идеальные пропорции. Работа вызвала бурные обсуждения.
Где используются числа Фибоначчи
Числа Фибоначчи — не просто математическая последовательность, а универсальный язык гармонии, связывающий науку, искусство, архитектуру и природу. Их применение показывает, как даже абстрактные формулы могут отражать фундаментальные законы мироздания.
Архитектура
Многие древние архитектурные сооружения выполнены по канонам золотого сечения. Ученые до сих пор спорят, применялись ли эти правила целенаправленно или нет.
Так, в древнегреческом храме Парфенон соотношение высоты фронтона к высоте фасада и расстояния между колоннами приближены к значению φ (фи).

Считается, что пропорции золотого сечения есть в геометрии пирамиды Хеопса, так как боковая грань пирамиды равна квадрату ее высоты.
Искусство
Золотое сечение делает любой предмет искусства особенно притягательным, ведь он становится максимально гармоничным для восприятия. Хотя его применение часто становится предметом дискуссий, есть примеры, в которых искусствоведы усматривают использование числа фи.
Иллюстрации Леонардо да Винчи украсили книгу Луки Пачоли «О божественной пропорции» (1509 года), где он детально исследовал математические основы гармонии.
Также считается, что Сальвадор Дали сознательно встроил золотое сечение в работу «Тайная вечеря». Холст имеет форму золотого прямоугольника, а ключевые элементы, например, фигуры святых и двенадцатигранник на фоне — выстроены по спирали Фибоначчи. Исследователи считают, что художник не раз использовал математические приемы в работах.

Есть и спорные случаи применения вычислений при создании произведений. Такие картины, как «Мона Лиза» Леонардо да Винчи или «Рождение Венеры» Сандро Боттичелли связывают с числом фи, но прямых доказательств авторы не оставили. Эксперты находят соответствия в построении композиции, однако это может быть совпадением или интуитивным чувством пропорции у художников.
Числа Фибоначчи и тесно связанное с ними золотое сечение применяют в самых разных областях, от природы и искусства до торговли на финансовых рынках. Считается, что в музыке Иоганна Себастьяна Баха золотое сечение использовалось для расположения кульминации музыкального произведения. Вероятно, композитор делал это по интуиции.
Дизайн и реклама
Принцип золотого сечения активно применяется в современном дизайне и рекламе. Яркий пример — логотип компании Apple. Отношение диаметра «надкусанного» яблока к его высоте равно примерно 1,618. А в иконке ВКонтакте круг и галочка вписаны в золотой прямоугольник.

Трейдинг
Числовую последовательность используют в математике и информатике для решения задач, а также в трейдинге. По словам эксперта, на финансовых рынках числа Фибоначчи используют для прогноза вероятных разворотов цены.
— Есть интересный эффект, который заключается в том, что если достаточно большое количество игроков на рынке верит в значимость определенного уровня (например, уровня Фибоначчи) и размещает там ордера на покупку или продажу, то цена действительно начинает реагировать на этот уровень, даже если с точки зрения экономики он не имеет объективного значения, — поясняет Василий Новицкий.
Главное о числах Фибоначчи
Числа Фибоначчи и золотое сечение — удивительные математические явления, которые пронизывают нашу реальность, начиная от растений и заканчивая шедеврами искусства. Это напоминание, что мир гораздо более упорядочен, чем кажется, а математика — универсальный язык гармонии мира.
- Числа Фибоначчи ― последовательность, где каждое число равно сумме двух предыдущих (0, 1, 1, 2, 3, 5…).
- Впервые упоминаются в задаче Фибоначчи о кроликах из книги 1202 года, но корнями уходят в древность.
- Золотое сечение ― предел отношения соседних чисел ≈1,618.
- Явление встречается в природе, анатомии, искусстве и технологиях, включая алгоритмы, финансы и дизайн.




