
К любому числу можно прибавить единицу, поэтому в строгом смысле самого большого числа не существует. Но есть рамки определенных систем описания, в пределах которых ученые создавали и создают числа-рекордсмены.
- Гугол и гуголплекс — это очень большие, но все же записываемые числа, выражающиеся через степени десятки.
- Числа Мозера, Райо, Грэма и TREE(3) настолько велики, что их невозможно выразить ни в десятичной форме, ни в экспоненциальной записи — требуются специальные нотации или описания.
- TREE(3) — одно из самых масштабных известных чисел, настолько большое, что делает все остальные на его фоне пренебрежимо малыми.
- Классические большие числа (миллион, миллиард, триллион и далее до дециллиона) представляют собой степени десяти и применяются в статистике, науке и быту.
- Некоторые огромные числа имеют практическое значение — например, число атомов во Вселенной (около 10⁸⁰) или криптографический предел 2²⁵⁶ (около 10⁷⁷).
Рассказываем о самых больших числах подробно.
7 экстремально больших чисел
За пределами знакомых нам миллиардов и триллионов есть гиганты, которые фундаментально меняют понимание «большого». Начнем с числа, наименование которого перекликается с названием известной поисковой системы.
1. Гугол

Гугол — это десятка в сотой степени (10100). Название этому числу придумал девятилетний мальчик Милтон Сиротта, дядей которого был американский математик Эдвард Казнер. В 1938 году во время прогулки ученый рассказывал племянникам о больших числах. Тогда Милтон придумал это необычное слово для наименования единицы со 100 нулями.
2. Гуголплекс
Если возвести десятку в степень гугол (10гугол), получится еще одно гигантское число — гуголплекс. Это единица с гуголом нулей. Название гуголплексу дал все тот же Милтон Сиротта, а в 1940 году Эдвард Казнер вместе с другим математиком Джеймсом Ньюманом рассказали об этих числах в своей книге «Новые названия в математике».
3. Число Скьюза
Число Скьюза — это наименьшее натуральное число, с которого нарушается одно важное неравенство в математике: π(n) < Li(n), где π(n) — функция распределения простых чисел, а Li(n) — сдвинутый интегральный логарифм.
В 1933 году южноафриканский математик Стэнли Скьюз нашел верхнюю границу для самого первого значения, где это неравенство нарушается. Так появилось число Скьюза.
Это одно из самых больших чисел, которое когда-либо использовалось в серьезном математическом доказательстве. Предполагается, что оно находится между 1019 и 1,3971672 x 10316 ≈ e727,951336108.
4. Число Райо
26 января 2007 года между профессорами Августином Райо и Адамом Эльгой состоялось соревнование — «Дуэль больших чисел». Райо победил, сформулировав такое определение: «Самое маленькое число, большее, чем любое конечное число, определенное выражением на языке теории множеств с использованием гугола символов или меньше».
Теперь одно из самых больших чисел названо фамилией Райо. Его невозможно записать ни в десятичной форме, ни с помощью степеней, ни даже с помощью самых мощных нотаций.
5. Число Мозера
В середине XX века математик Лео Мозер придумал необычный способ записи гигантских чисел с помощью геометрических фигур. Число Мозера — это результат многократного возведения двойки в степень самой себя. Количество вложенных операций задается через специальные символы (треугольники, квадраты, круги), каждый из которых означает новый, невероятно мощный уровень этой вложенности. «Два в круге» — это и есть этот рекордсмен. Его невозможно осознать или записать в обычной десятичной форме.
6. Число Грэма
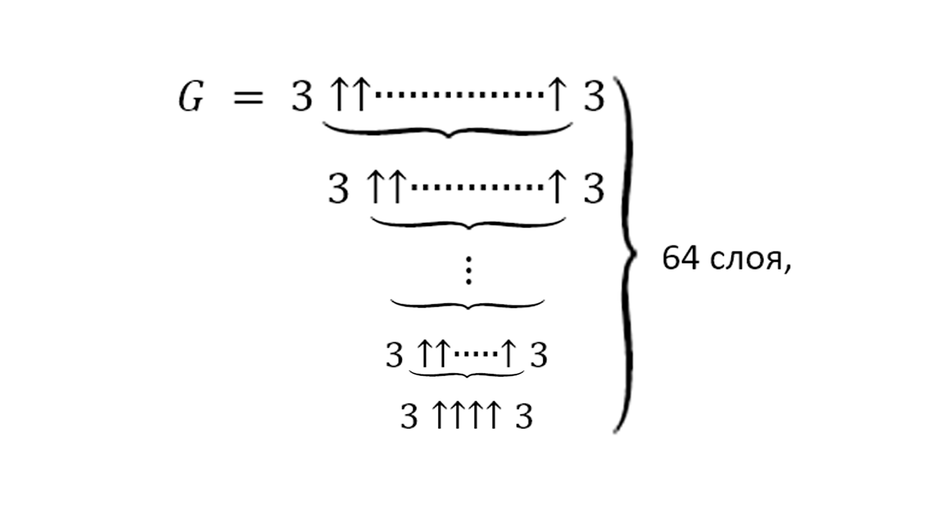
Это легендарный гигант, который в XX веке попал в Книгу рекордов Гиннесса. Математик Рональд Грэм ввел его в 1970-х для решения сложной комбинаторной задачи. Отобразить его в обычном десятичном виде невозможно, поэтому для записи приходится использовать специальный способ — нотацию Кнута, где каждая новая стрелка обозначает мощную операцию.
7. TREE(3)
TREE (3) — число из теории графов, которое появилось в ходе исследований математика Харви Фридмана. Его величина абсолютно невообразима: оно делает число Грэма исчезающе малой пылинкой. Даже мощнейшие стрелочные нотации Кнута и Конвея бессильны адекватно записать TREE(3). Масштаб числа таков, что разные уровни огромности «размываются» — их очень сложно осмыслить.
Какие классические числа считаются самыми большими
Когда мы говорим о классических больших числах, речь обычно идет о степенях десятки.
1. Миллион
Единица с шестью нулями, или 106. Примерно столько жителей в крупном городе вроде Волгограда, Воронежа или Перми.
2. Миллиард
За миллионом следует миллиард — единица с девятью нулями, или 109. 4,5 млрд лет — примерно таков возраст планеты Земля.
3. Триллион
После миллиарда идет триллион. Это единица с 12 нулями, или 1012. По оценкам масштабных исследований, на нашей планете растет примерно три триллиона деревьев.
4. Квадриллион
Квадриллион — это 1015, то есть единица с 15 нулями. В пяти граммах плодородной почвы может содержаться до одного квадриллиона бактериальных клеток.
5. Квинтиллион
Следующий на очереди — квинтиллион, или единица с 18 нулями (1018). Количество насекомых на нашей планете равно 10 квинтиллионам.
6. Секстиллион
Далее — единица с 21 нулем, или 1021. Примерно столько молекул содержится в одной капле воды массой 0,03 мл.
7. Септиллион
За секстиллионом идет септиллион — 1024. Единица с 24 нулями — этому числу равно количество звезд в той части Вселенной, которую мы можем наблюдать.
8. Октиллион
После септиллиона следует октиллион — единица с 27 нулями, или 1027. Масса земной коры оценивается примерно в 26 октиллионов.
9. Нониллион
Нониллион — это 1030, или единица с 30 нулями. Общее количество бактерий на земном шаре составляет примерно пять нониллионов.
10. Дециллион
Единица с 33 нулями — это дециллион (1033). Такие масштабы сложно вообразить, но примерно 12 дециллионов джоулей — это энергия, которую Солнце излучает за год.
Вопросы и ответы
Ответим на часто возникающие вопросы о больших числах.
Какое натуральное число самое большое?
Математика дает однозначный ответ: наибольшего натурального числа нет. Это фундаментальное свойство натурального ряда — он бесконечен. Какое бы гигантское число вы ни назвали, всегда можно записать его плюс один.
Какое простое число самое большое?
Простое число — это натуральное число больше единицы, которое делится только на единицу и само на себя. Их ряд бесконечен. Однако математики и энтузиасты постоянно ищут все более крупные известные простые числа. В 2025 году самое известное простое число — это 2136 279 841 − 1.
Существует ли самое большое число, которое имеет практический смысл?
Да, и оно зависит от области применения. Например, в космологии это ~1080 (атомы в видимой Вселенной). В криптографии — ~1077 (2256, «невзламываемый» предел). В вычислениях подобный статус получило ~1018, которое обозначает предел точности для обычных операций.





